Le concept de dimension n’a l’air de rien quand on le découvre au lycée: un espace à une dimension est un axe tout simplement, à deux dimensions c’est une surface plane, en trois dimensions on ajoute la notion de profondeur. On n’arrive pas bien à se représenter quatre dimensions, mais mathématiquement ça n’est jamais qu’un monde où les vecteurs ont quatre coordonnées au lieu de trois, et ainsi de suite. Mais derrière leur similitude de façade, ces différents mondes imbriqués les uns dans les autres comme des poupées russes exhibent parfois des particularités mathématiques très déroutantes…
Le cochonnet géant
Commençons par balayer quelques idées préconçues sur la taille des objets. Prenez un carré de côté 4 et tracez à l’intérieur quatre cercles de diamètre 1 tangents entre eux et aux bords du carré. Au centre il reste un peu de place pour dessiner un petit cercle (en bleu), tangent aux quatre cercles voisins. Vous pouvez imaginer le même montage en dimension 3, avec quatre huit boules de pétanques rangées dans une boite cubique et un cochonnet au milieu:
Que se passe-t-il dans un hypercube de dimension n rempli d’hypersphères? Ne vous faites pas une entorse du cerveau en essayant de le dessiner, calculons juste le rayon du « petit » cercle central:  Aussi bizarre que ça puisse paraître, à mesure que le nombre de dimensions augmente le cochonnet au centre devient de plus en plus grand, tout en restant tangent aux hyperboules voisines. En quatrième dimension l’hypercochonnet est aussi grand qu’elles. Dès la dixième dimension son rayon vaut √10 -1, il est donc plus grand que l’hyperboîte. Si on augmente encore le nombre de dimensions, l’essentiel de son volume est même à l’extérieur de cet hypercube!
Aussi bizarre que ça puisse paraître, à mesure que le nombre de dimensions augmente le cochonnet au centre devient de plus en plus grand, tout en restant tangent aux hyperboules voisines. En quatrième dimension l’hypercochonnet est aussi grand qu’elles. Dès la dixième dimension son rayon vaut √10 -1, il est donc plus grand que l’hyperboîte. Si on augmente encore le nombre de dimensions, l’essentiel de son volume est même à l’extérieur de cet hypercube!
La conjecture de la saucisse
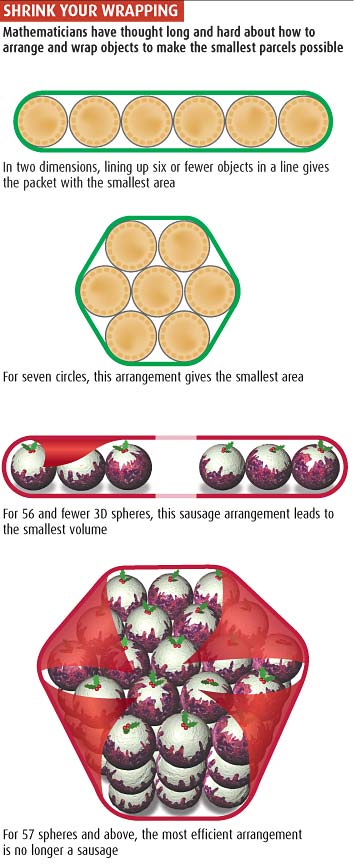
Source: New Scientist
Bientôt Noël! Vous avez vu un peu juste en papier cadeau, il va donc falloir être économe en emballage. Heureusement, vous n’avez que des trucs ronds à emballer: des disques (à emballer « à plat » et non pas empilés), des balles de tennis et même -après tout c’est Noël- des hypersphères d’un peu toutes les dimensions. Comment allez-vous vous y prendre?
Commençons par les disques plats (dimension 2): jusqu’à 6 disques, le mieux est de les emballer alignés les uns derrière les autres, comme une chenille de char. Mais dès que vous en avez 7 ou plus, mieux vaut les grouper en hexagone…
Les balles de tennis maintenant (dimension 3). Personnellement je les aurais empilées… et j’aurais eu tout faux car la forme pyramidale n’est optimale qu’à partir de 57 balles. Si votre cadeau est moins généreux, il vaut mieux opter pour le format « aligné » (comme comme sur le dessin) qui fait ressembler le paquet à une sorte de saucisse, très sobre en emballage.
Pour vos hypersphères en quatre dimensions, même chose: tant que vous offrez moins de 50 000 hyper-balles de tennis, vous devriez les emballer alignées au format « hyper-saucisse ». Au-delà c’est moins clair. Pour 100 000 hypersphères une forme arrondie est plus optimale, mais on n’a pas trouvé quel est le meilleur emballage ni le seuil à partir duquel l’hyper-saucisse n’est plus la meilleure solution…
En cinquième dimension et au-delà, plus de question à se poser! Le mathématicien Fejes Thot est convaincu que la saucisse est toujours plus avantageuse, quel que soit le nombre d’hypersphères. A ce jour on a réussi à démontrer sa conjecture pour les dimensions supérieures à 42 (!), mais pas encore pour celles qui sont comprises entre 5 et 41…
L’épicier et ses hyper-oranges
C’est bien beau d’économiser le papier cadeau, mais comment rentre-t-on ces énormes paquets sous le sapin? Le problème du rangement optimal des sphères est une question célèbre qui agite les neurones des mathématiciens depuis longtemps. Déjà en 1610 Kepler conjectura en regardant son épicier empiler des oranges, que la forme pyramidale était la plus compacte en volume. Ça semble évident mais il fallut attendre 350 ans pour qu’on arrive à démontrer ce résultat en 1998.

Empilement optimal de 35 sphères. Source Wikipedia
Passons aux dimensions supérieures. En dimension 4, cet empilement est encore le meilleur et c’est vrai en dimension 5, 6, 7, 8, 9, 10…. Mais n’allez pas conclure trop vite! Cette méthode est optimale dans toutes les dimensions… sauf UNE: la dimension 24. En 1965 John Leech découvrit une manière encore plus économique d’empiler des hyper-oranges de 24 dimensions, et sa méthode ne fonctionne que pour cette dimension et pas une autre.
Pourquoi 24 et pas 23 ni 25? Personne n’en sait rien mais en théorie des groupes -la branche mathématique à laquelle appartient ce problème- ce genre de bizarreries est plus que fréquente. Chaque dimension possède sa ménagerie particulière de groupes de symétrie. A titre d’exemple, le groupe de symétrie le plus complexe qu’on connaisse (qu’on surnomme le groupe Monstre) n’existe que dans un espace à 196 884 dimensions!
La dégénerescence des hypercomplexes
Cette dégénérescence des grandes dimensions est courante en algèbre. Souvenez-vous de la construction des nombres complexes. On part des nombres réels qui forment un espace à une dimension. A partir d’une paire de réels, on définit le plan des nombres complexes qui s’additionnent et se multiplient parfaitement et dont la racine est toujours définie (c’est bien l’intérêt). Seul petit bémol, ils ne se comparent plus (i n’est ni plus grand ni plus petit que 1).
Une fois qu’on sait construire les nombres complexes, il semble naturel de partir à la conquête des dimensions supérieures. Pourrait-on trouver un espace en trois dimensions où l’on puisse additionner et multiplier des triplets de nombres? Hamilton fut le premier à essayer et il se cassa les dents sur cette question. Par contre, il découvrit en 1843 qu’on n’a pas ce problème dans la quatrième dimension. Mais les quaternions ainsi créés souffrent d’une maladie congénitale: leur produit n’est pas commutatif (A*B n’est pas égal à B*A). Un peu comme les rotations dont la combinaison est commutative dans le plan mais pas dans l’espace: l’ordre des rotations est important quand on joue au Rubik’s Cube!
Pour grimper dans les dimensions supérieures, il faut rééditer la ruse de Hamilton et doubler la dimension à chaque étape. Mais c’est au prix d’une dégénérescence de plus en plus grave: en dimension 8, voici les octonions dont le produit n’est plus associatif: A*(B*C) ne vaut pas (A*B)*C. La dimension 16 est encore plus étrange puisque ses sédénions sont divisibles par zéro! Dans un tel espace il est impossible de définir une « norme », c’est-à-dire de mesurer quoi que ce soit. Les mathématiciens ont du coup renoncé à aller plus loin dans leur quête…
| dimension | nom | limite |
|---|---|---|
| 1 | réels | – |
| 2 | complexes | perte de la comparaison |
| 4 | quaternions | perte de la commutativité |
| 8 | octonions | perte de l’associativité |
| 16 | sédénions | perte de la mesure |

Le monde des hypercomplexes vus par Karim
L’étrange zoologie des polytopes
A l’inverse, les grandes dimensions permettent (parfois) de simplifier les choses. Visitons par exemple le zoo des figures régulières (convexes) de la géométrie classique, tels que les polygones, les polyèdres etc.
– En dimension 1, il n’y a qu’une seule figure régulière finie: le segment. Un monde uniforme et ennuyeux…
– En dimension 2, on construire un polygone régulier, en assemblant de façon symétrique plusieurs segments égaux. Il y a une infinité de polygones différents car on peut choisir n’importe quel nombre de segments. Liberté totale!
– En dimension 3, les polyèdres réguliers s’obtiennent en assemblant symétriquement des polygones réguliers. Le retour à l’ordre est sévère car il n’y a plus que cinq possibilités, les fameux solides de Platon:
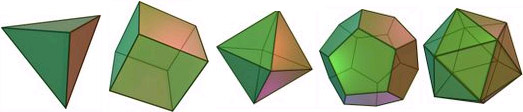
Les cinq polyèdres convexes de Platon: tétraèdre, cube, octaèdre, dodécaèdre et icosaèdre. Source ici
Seuls le triangle, le carré et le pentagone ont droit de cité en dimension 3, les autres polygones (hexagone, heptagone etc.) se contentent d’une existence plate et sans relief. – En dimension 4, on parle de « polytopes réguliers » qu’on construit en assemblant symétriquement des polygones réguliers de dimension 3. Il n’y en que a six, toujours à base de triangles, de carrés et de pentagones, avec des noms que le Capitaine Haddock n’aurait pas renié. Regardez par exemple cet hécatonicosachore, un assemblage de 120 dodécaèdres!

Différents points de vue sur un hécatonicosachore en 4D. Source Wikipedia
– En dimension 5 et au-delà, les choses se régularisent et se simplifient brusquement (façon de parler). Il n’y a plus que trois polytopes réguliers: les n-simplexes (définis à partir de tétraèdres) les hypercubes et les hyper-octaèdres. Je me suis amusé à tracer un arbre généalogique de toutes ces figures:  Le nombre de figures dans chaque dimension suit donc une suite étrange: 1, ∞, 5, 6, 3, 3, 3, 3… Je ne peux m’empêcher de faire le parallèle avec l’arbre phylogénétique du vivant lors de l’explosion précambrienne (dont on avait parlé ici): après une extinction massive (une seule figure en dimension 1), le nombre de familles explose littéralement (une infinité de polyèdres en dimension 2), puis il se réduit fortement (cinq en dimension 3, six en dimension 4, trois en dimension 5), avant de se stabiliser (trois dans les dimensions supérieures).
Le nombre de figures dans chaque dimension suit donc une suite étrange: 1, ∞, 5, 6, 3, 3, 3, 3… Je ne peux m’empêcher de faire le parallèle avec l’arbre phylogénétique du vivant lors de l’explosion précambrienne (dont on avait parlé ici): après une extinction massive (une seule figure en dimension 1), le nombre de familles explose littéralement (une infinité de polyèdres en dimension 2), puis il se réduit fortement (cinq en dimension 3, six en dimension 4, trois en dimension 5), avant de se stabiliser (trois dans les dimensions supérieures).

Source ici
Tout comme l’arbre du vivant -et contrairement à ce qu’on a vu pour l’algèbre – seules les géométries très « régulières » échappent à l’extinction progressive en dimensions élevées. On le voit au nombre de cellules de ces polytopes: les survivants suivent des règles simples: n+1 cellules pour les n-simplexes, 2n pour les hyper-octaèdres, 2n pour les hypercubes. Tous les autres qui étaient régis par des formules exotiques ont disparu. La géométrie serait-elle allergique aux noms imprononçables? J’arrête là ma collection de bizarreries dimensionnelles. Et vous, laquelle préférez-vous? En connaissez-vous d’autres?
Ian Stewart: Mon Cabinet de Curiosités Mathématiques (pour la conjecture de la saucisse)
Marcus du Sautoy: les symétries ou les maths au clair de lune pour les étranges groupes de symétrie
La page de Wikipedia sur les polytopes en dimension 4 et celle sur les nombres hypercomplexes
Billets connexes
Dans combien de dimensions vivons-nous, un billet complémentaire sur les miracles de la dimension 3
E dans l’O: la géométrie de l’électromagnétisme: qui explique pourquoi l’électromagnétisme est une émanation de la troisième dimension


19 comments for “Surprenantes dimensions”